Class 8 Math Rational Numbers Notes

Rational Numbers – Class 8

Hi kids! This chapter is all about numbers called Rational Numbers. Don’t worry, they’re not as scary as they sound!

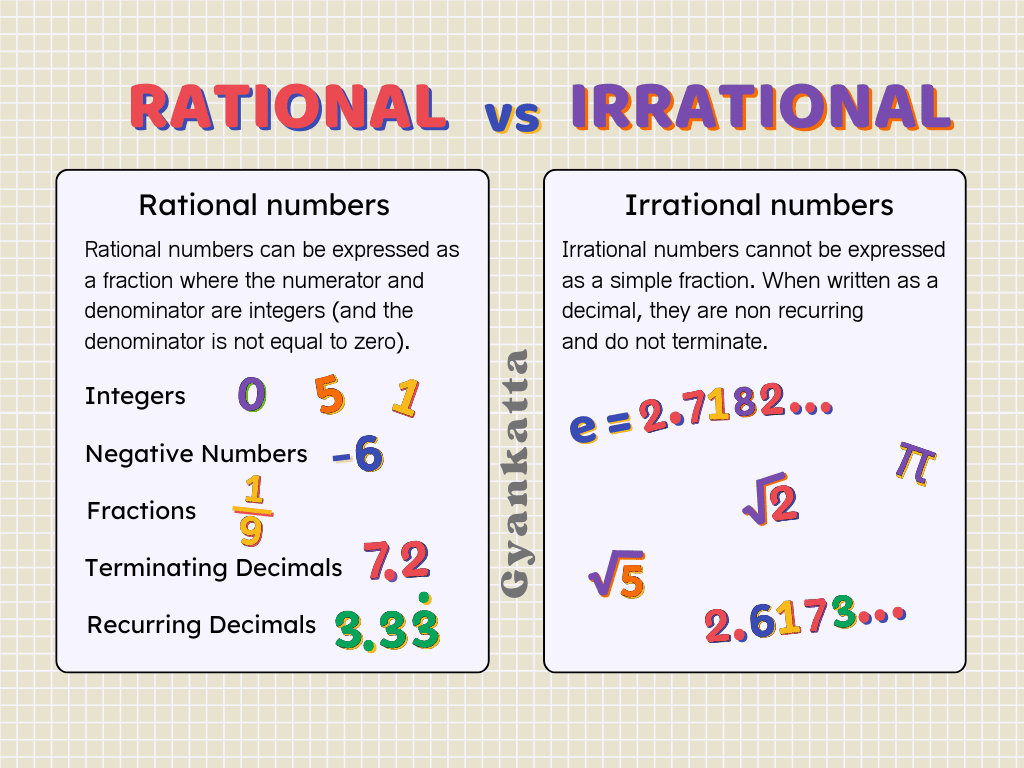
What are Rational Numbers?

A rational number is any number that can be written as a fraction, where both the top (numerator) and bottom (denominator) are whole numbers, and the bottom number is not zero.

Examples: 1/2, 3/4, -2/5, 7, 0, -10/3

Non-Examples: √2 (square root of 2), π (pi)

Think of it like sharing a pizza! If you cut a pizza into 8 slices, and you take 3, you have 3/8 of the pizza. That’s a rational number!

Properties of Rational Numbers

1. Closure Property:

When you add, subtract, multiply, or divide (except by zero) two rational numbers, the answer is always another rational number.

2. Commutative Property:

You can add or multiply rational numbers in any order. The result stays the same.

Example: 1/2 + 2/3 = 2/3 + 1/2

Example: 1/2 * 2/3 = 2/3 * 1/2

3. Associative Property:

When adding or multiplying three or more rational numbers, you can group them in any way you like. The result stays the same.

Example: (1/2 + 1/3) + 1/4 = 1/2 + (1/3 + 1/4)

Example: (1/2 * 1/3) * 1/4 = 1/2 * (1/3 * 1/4)

4. Distributive Property:

Multiplication distributes over addition. This means a(b + c) = ab + ac

Example: 1/2 * (1/3 + 1/4) = (1/2 * 1/3) + (1/2 * 1/4)

5. Identity Property:

Adding 0 to any rational number doesn’t change it. Multiplying any rational number by 1 doesn’t change it.

Example: 5 + 0 = 5

Example: 5 * 1 = 5

6. Inverse Property:

Every rational number has an additive inverse (opposite) and a multiplicative inverse (reciprocal).

Additive inverse of 3 is -3. 3 + (-3) = 0

Multiplicative inverse of 2/3 is 3/2. (2/3) * (3/2) = 1

Operations on Rational Numbers

1. Addition:

To add fractions with the same denominator, add the numerators. If they have different denominators, find a common denominator first.

2. Subtraction:

Similar to addition, but subtract the numerators.

3. Multiplication:

Multiply the numerators and multiply the denominators.

4. Division:

To divide by a fraction, multiply by its reciprocal.

Keep practicing, and you’ll become a rational number whiz!

Rational Numbers Questions

1. Which of the following is a rational number?

a) √3 b) 0 c) π d) √5

b) 0

0 can be written as 0/1, which fits the definition of a rational number (a fraction where the denominator is not zero). Square roots of non-perfect squares (like √3 and √5) and pi (π) are not rational.

2. What is the additive inverse of -4/7?

4/7

The additive inverse of a number is its opposite. Adding a number and its additive inverse always results in 0.

3. What is the multiplicative inverse (reciprocal) of 5/2?

2/5

The multiplicative inverse of a number is the number you multiply it by to get 1. To find the reciprocal, simply flip the fraction.

4. Simplify: 2/3 + 1/4

11/12

Find a common denominator (12). (2/3)*(4/4) + (1/4)*(3/3) = 8/12 + 3/12 = 11/12

5. Simplify: 3/5 – 1/2

1/10

Find a common denominator (10). (3/5)*(2/2) – (1/2)*(5/5) = 6/10 – 5/10 = 1/10

6. Simplify: (2/3) * (3/4)

1/2

Multiply the numerators and multiply the denominators: (2*3)/(3*4) = 6/12. Then simplify to 1/2.

7. Simplify: (4/5) ÷ (2/3)

6/5 or 1 1/5

To divide fractions, multiply by the reciprocal of the second fraction: (4/5) * (3/2) = 12/10. Simplify to 6/5 or the mixed number 1 1/5.

8. Which property is illustrated by: 2/5 + 3/5 = 3/5 + 2/5?

Commutative Property of Addition

The order of addition doesn’t change the result.

9. Which property is illustrated by: (1/2) * (2/3 + 1/4) = (1/2 * 2/3) + (1/2 * 1/4)?

Distributive Property

Multiplication distributes over addition.

10. Is -7/8 greater than -5/6?

To compare, find a common denominator (-24). -7/8 becomes -21/24 and -5/6 becomes -20/24. -20/24 is greater than -21/24. So, -5/6 is greater than -7/8.