Class 8 Math Mensuration Notes
Mensuration – Class 8
Hi everyone! This chapter is all about Mensuration. We’ll learn how to calculate the areas and volumes of different shapes. These skills are very useful in real life!
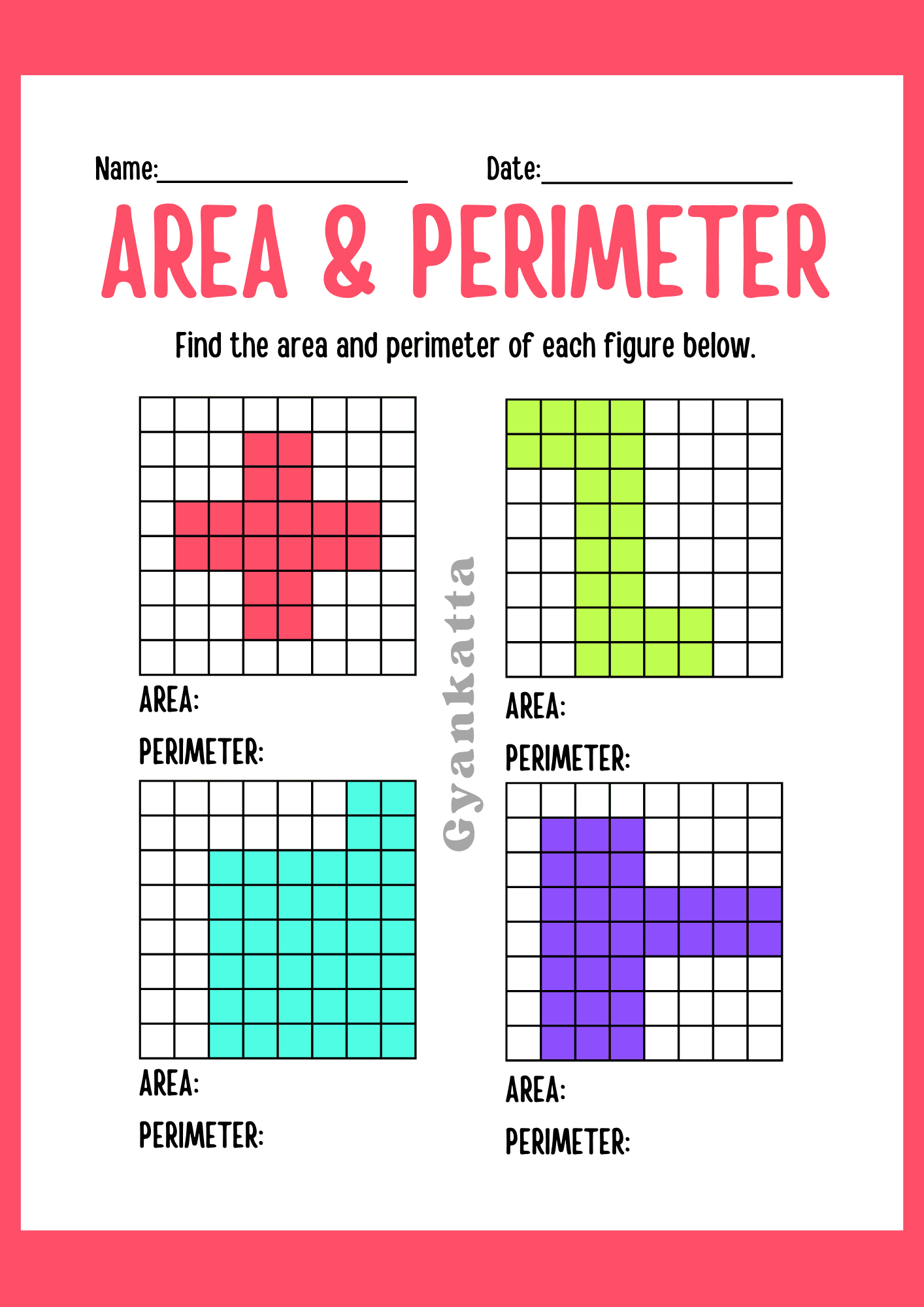
1. Area of 2D Shapes
a) Rectangle:
Area = Length × Width
Example: A rectangular garden is 10m long and 5m wide. Its area is 10m × 5m = 50 sq m.
b) Square:
Area = Side × Side (Side²)
Example: A square tile has a side of 30cm. Its area is 30cm × 30cm = 900 sq cm.
c) Triangle:
Area = (1/2) × Base × Height
Example: A triangle has a base of 8cm and a height of 6cm. Its area is (1/2) × 8cm × 6cm = 24 sq cm.
d) Parallelogram:
Area = Base × Height
Example: A parallelogram has a base of 10cm and a height of 5cm. Its area is 10cm × 5cm = 50 sq cm.
e) Circle:
Area = πr² (where π ≈ 3.14 and r is the radius)
Example: A circle has a radius of 7cm. Its area is approximately 3.14 × 7cm × 7cm = 153.86 sq cm.
f) Trapezium:
Area = (1/2) × (Sum of parallel sides) × Height
Example: A trapezium has parallel sides of 10cm and 12cm, and a height of 8cm. Its area is (1/2) × (10cm + 12cm) × 8cm = 88 sq cm.
2. Volume of 3D Shapes
a) Cube:
Volume = Side × Side × Side (Side³)
Example: A cube has a side of 4cm. Its volume is 4cm × 4cm × 4cm = 64 cubic cm.
b) Cuboid:
Volume = Length × Width × Height
Example: A cuboid is 5m long, 3m wide, and 2m high. Its volume is 5m × 3m × 2m = 30 cubic m.
c) Cylinder:
Volume = πr²h (where π ≈ 3.14, r is the radius, and h is the height)
Example: A cylinder has a radius of 7cm and a height of 10cm. Its volume is approximately 3.14 × 7cm × 7cm × 10cm = 1538.6 cubic cm.
Applications of Mensuration
1. Construction:
Calculating the amount of material needed for building projects (e.g., bricks, cement, paint).
2. Packaging:
Designing boxes and containers to hold products efficiently.
3. Gardening:
Calculating the area of a garden to determine how much fertilizer or seed is needed.
4. Everyday Life:
Estimating the size of carpets, curtains, or other household items.
Mensuration is a practical skill that helps us measure and understand the world around us.
Mensuration Quiz – Application Problems
1. Carpet Area: A rectangular room is 5 meters long and 4 meters wide. How much carpet is needed to cover the floor?
2. Garden Fence: A square garden has a side length of 8 meters. How much fencing is needed to enclose the garden?
3. Triangular Flag: A triangular flag has a base of 1.2 meters and a height of 0.8 meters. What is the area of the flag?
4. Park Design: A park is shaped like a parallelogram with a base of 20 meters and a height of 15 meters. What is the area of the park?
5. Circular Tablecloth: A circular table has a radius of 1 meter. How much fabric is needed to make a tablecloth for the table (π ≈ 3.14)?
6. Trapezoidal Field: A field is shaped like a trapezium. The two parallel sides are 30 meters and 40 meters long, and the distance between them is 20 meters. What is the area of the field?
7. Cube-Shaped Box: A cube-shaped box has a side length of 6 cm. What is the volume of the box?
8. Rectangular Tank: A rectangular water tank is 2 meters long, 1.5 meters wide, and 1 meter high. What is the volume of the tank?
9. Cylindrical Container: A cylindrical container has a radius of 7 cm and a height of 10 cm. What is the volume of the container (π ≈ 3.14)?
10. Swimming Pool: A swimming pool is 20 meters long, 10 meters wide, and has an average depth of 2 meters. What is the volume of water the pool can hold?


