Class 8 Math Algebraic Expressions and Identities Notes
Algebraic Expressions and Identities – Class 8
Hi everyone! This chapter introduces Algebraic Expressions and Identities. These are powerful tools for solving math problems and understanding patterns.
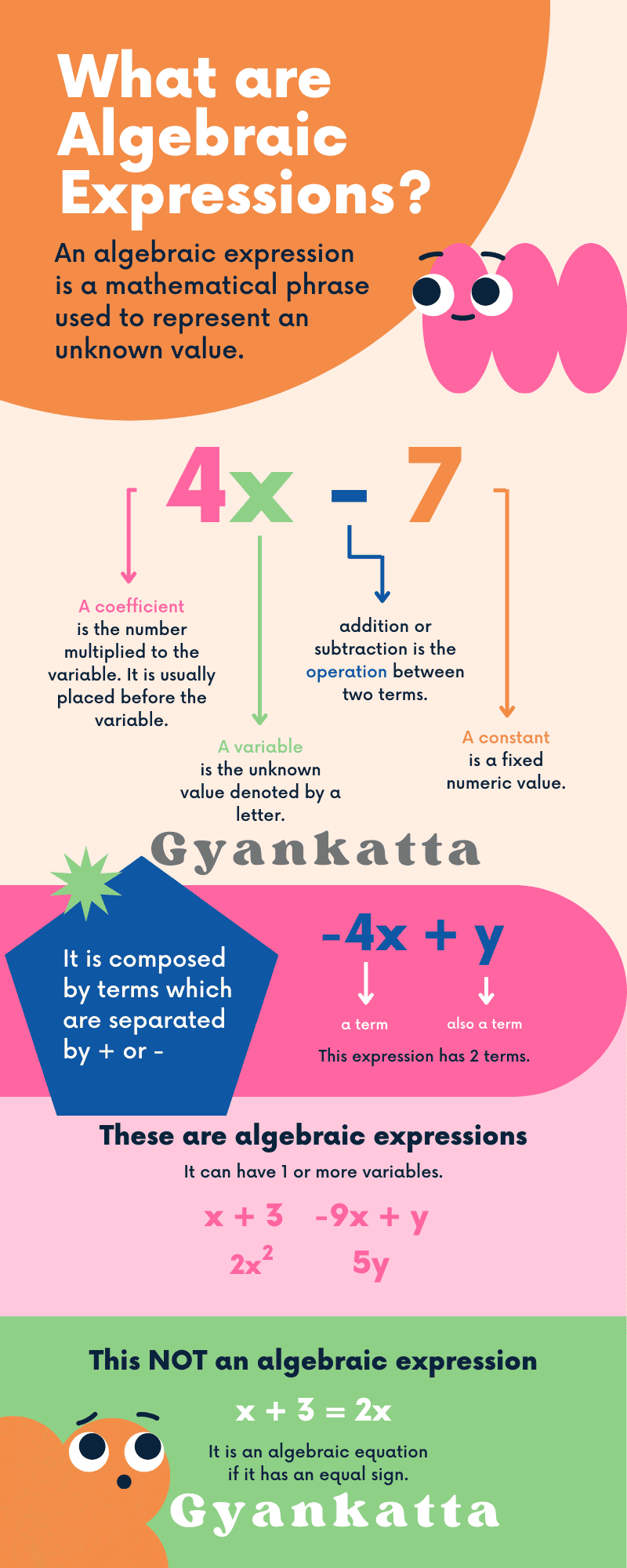
What are Algebraic Expressions?
An algebraic expression is a combination of variables (like x, y, z), constants (like 2, 5, -3), and operations (like +, -, ×, ÷). It doesn’t have an equals sign.
Examples: 2x + 3, 5y – 7z, x² + 2xy + y²
Terms:
Parts of an expression separated by ‘+’ or ‘-‘ signs.
In 2x + 3, ‘2x’ and ‘3’ are terms.
Coefficients:
The numerical factor of a term.
In 2x, ‘2’ is the coefficient.
Variables:
Letters that represent unknown values.
In 2x, ‘x’ is the variable.
What are Identities?
An identity is an equation that is true for all values of the variables. It’s a formula that always works.
Example: (a + b)² = a² + 2ab + b² is an identity.
Important Identities
Here are some identities you should know:
- (a + b)² = a² + 2ab + b²
- (a – b)² = a² – 2ab + b²
- (a + b)(a – b) = a² – b²
- (x + a)(x + b) = x² + (a + b)x + ab
Applications of Algebraic Expressions and Identities
1. Geometry:
Finding areas and volumes of shapes. For example, the area of a square with side (x + 2) can be found using the identity (a+b)².
2. Simplifying Calculations:
Identities can make complex calculations easier. For example, calculating 102² can be done as (100+2)² which is easier to calculate using the identity.
3. Problem Solving:
Algebraic expressions and identities are used to solve a variety of word problems in algebra and other areas of mathematics.
4. Computer Programming:
These concepts are fundamental to computer programming and are used in writing algorithms and solving computational problems.
Understanding algebraic expressions and identities is crucial for further studies in mathematics and related fields.
Algebraic Expressions and Identities Quiz – Application Problems
1. Area of a Square: A square garden has a side length of (x + 3) meters. What is the area of the garden?
2. Area of a Rectangle: A rectangular playground has a length of (2x + 5) meters and a width of (x – 2) meters. What is the area of the playground?
3. Simplifying an Expression: A shopkeeper buys (3x + 2) items at Rs. (x + 5) each. What is the total cost?
4. Volume of a Cube: A cube has a side length of (2x – 1) cm. What is the volume of the cube?
5. Difference of Squares: A rectangular field has an area of (x² – 25) square meters. If the length of the field is (x + 5) meters, what is the width of the field?
6. Cost of Fencing: A square garden has a side length of (x + 4) meters. What is the cost of fencing the garden if the fencing costs Rs. 10 per meter?
7. Simplifying a Calculation: Use an identity to calculate 101².
8. Another Calculation: Use an identity to calculate 99 * 101.
9. Area of a Path: A rectangular park is (2x + 3) meters long and (x + 2) meters wide. There is a path of width 1 meter all around the park. Find the area of the path.
10. Factoring: The area of a square is given by the expression x² + 8x + 16. What is the side length of the square?

